L'addition est exacte à +/- 150 millièmes près, du fait de l'arrondi et de l'addition d'arrondi.
J'ai (enfin) calculé la distribution de probabilité de la différence entre le temps obtenu par addition et le temps réel:
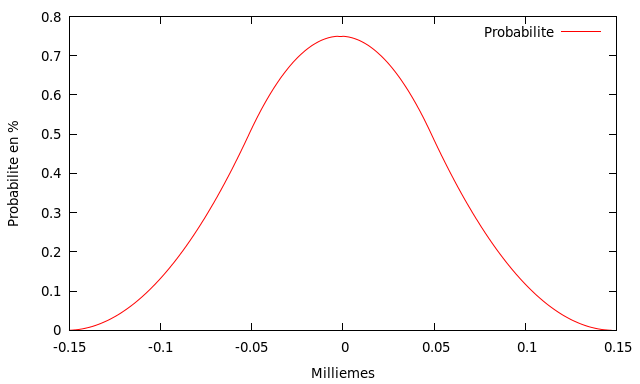
(Quasi gaussien, rien de surprenant)
(Gasp, j'ai gardé le temps en abscisses en secondes, je changerai !)
La probabilité que la valeur réelle soit dans le dixième* évalué par addition est de 66,66%.
La probabilité que la valeur réelle soit dans le dixième inférieur** à celui évalué par addition est de 17,17%
La probabilité que la valeur réelle soit dans le dixième supérieur** à celui évalué par addition est de 16,17%
Ca n'est pas exactement symétrique parce que l'arrondi n'est pas symétrique.
Donc dans un peu moins de 2/3 des cas, le dixième évalué est le dixième juste.
C'est valable depuis que le dixième est arrondi au plus proche.
Auparavant le dixième était arrondi au dixième en dessous, les choses était un peu différente.
Hugues
*: C'est à dire entre -50 millièmes (compris) et +50 millièmes (exclu)
**: C'est à dire entre -150 millièmes (compris) et -50 millièmes (exclu)
***: C'est à dire entre +50 millièmes (compris) et 150 millièmes (exclu)
